入門統計学 3章 推定と誤差

#+beign_src R :tangle R-text/code/03.R 








標本分布 (http://wiki.cis.iwate-u.ac.jp/~suzuki/RforS/org/RforS-II-04.html より抜粋)








正規母集団






##
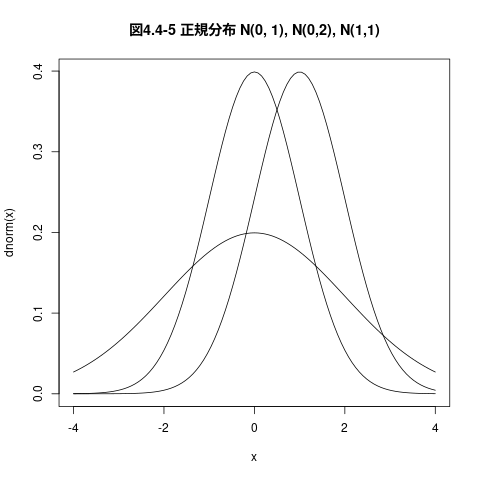
## 正規分布のグラフを描く
##

curve(dnorm(x), from=-4, to=4, main="図4.4-5 正規分布 N(0, 1), N(0,2), N(1,1)")        # 標準正規分布のグラフ， -4 から +4 の範囲
curve(dnorm(x,sd=2), add=TRUE)        # 平均0， 偏差2 の正規分布，上描き 
curve(dnorm(x,mean=1,sd=1), add=TRUE) # 平均1， 偏差1 の正規分布，上描き 









    

  • 図4.4-4.5 正規分布 N(0,1), N(0,2), N(1,1)
    

    


    

    04-04.png

    

    

    

    • 









正規母集団から単純無作為抽出を行なう





Rを使って正規分布の母集団から標本を抽出する方法





例えば、平均50、標準偏差10の正規母集団からn＝5の標本を無作為抽出
する






##
## 平均50、標準偏差10の正規母集団からn＝5の標本を無作為抽出する
##

rnorm(n=5, mean=50, sd=10)       # 標本の抽出
hist(rnorm(n=5, mean=50, sd=10), main="図4.7 N(50, 10)からの n=5 の標本の頻度表") # 頻度表の描画











図 4.7 N(50,10)からの n=5 の標本の頻度表







04-07.png








##
## 平均50、標準偏差10の正規母集団からn＝1000の標本を無作為抽出する

hist(rnorm(n=1000, mean=50, sd=10), main="図4.8 N(50, 10)からの n=1000 の標本の頻度表")













図 3.8 N(50,10)からの n=1000 の標本の頻度表







04-08.png














標本分布






標本分布
標本統計量の確率分布のこと


    

  • 推定値の信頼性の判断に用いる
    • 


  • 標本における個々のデータの実現値を表した度数分布ではなく、
    • 


  • 標本統計量の確率分布である
    • 










標本分布から何が分るのか





（1）標本分布が母数の本当の値を中心として分布しているか
（2）標本分布が横に大きく広がっていないか








標本分布を経験的に求める





標本分布は次のものから数学的に求まる:




    

  1. 母集団分布
    2. 

  2. 標本統計量の計算式 (変数変換)
    3. 

  3. 標本数
    4. 





Rを用いて，理論的ではなく，経験的の標本分布を求めることができる





標本統計量の実現値を大量に得られれば，そのヒストグラムは，標本分
布近いものとなるはず。




    

  • サイズ \( n \) の標本を何度も繰かえし抽出し，実現量を計算し，ヒス
トグラムを作成する
    • 





しかし，母集団分布が母数を含めてわかっていないため，




    

  • 「もし母集団分布がこのような正規分布だったら、
    • 


  • このくらいあてになる推定値が得られる」
    • 





ということを検討することになる。














正規母集団の母平均の推定




    

  • 母集団分布 \( \sim N(50, 10^2)\)
    • 

  • \( n = 10 \)
    • 

  • 母平均の推定量は，標本平均 \( \overline{X} \)
    • 






##
## 標本サイズ10の標本による，母平均の推定

標本 <- rnorm(n=10, mean=50, sd=10)
mean(標本)







44.9971134002593








標本平均の標本分布を求める





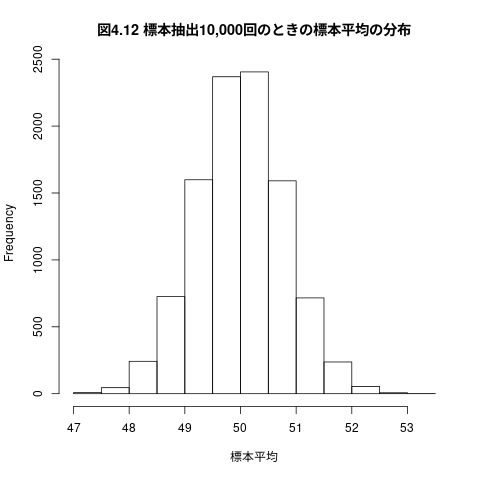
母平均の推定を10000回繰り返し





##
## 母平均の推定
### 母集団 N(50, 10^2) から
### 標本サイズ 10の標本の標本平均
### 10000個の標本平均の頻度表を描く
this.mean <- 50
this.sd <- 10
this.counts <- 10000

for (this.sample_size in c(10,20,40,80,160)) {
  標本平均 <- numeric(length=this.counts) 
      
  for(i in 1:this.counts) {
1
    標本 <- rnorm(n=this.sample_size, mean=this.mean, sd=this.sd)
    標本平均[i] <- mean(標本)
  }
  cat("sample_size=", this.sample_size,
      "mean=", mean(標本平均),
      "var=", var(標本平均),
      "\n")
}






sample_size= 10 mean= 49.96241 var= 10.05521 
sample_size= 20 mean= 50.0166 var= 4.972701 
sample_size= 40 mean= 50.00013 var= 2.492854 
sample_size= 80 mean= 49.98691 var= 1.258187 
sample_size= 160 mean= 50.0009 var= 0.6234049







hist(標本平均,main="図4.12 標本抽出10,000回のときの標本平均の分布")










図4.12 標本抽出10,000回のときの標本平均の分布






04-12.png







母平均 (50)からのズレが5以内か否かで振り分ける






## 母平均 (50)からのズレが5以内か否かで振り分ける

誤差絶対値5以下 <- ifelse( abs(標本平均-50) <= 5, 1, 0)
table(誤差絶対値5以下)


















0
1190





1
8810








88%くらいは，母平均+-5に収まっている




    

  • (n → inf) で \( E(\overline{X}) = \)母平均
    • 






##
## 10000個の標本平均の平均値

mean(標本平均)

## 10000個の標本平均の分散値

var(標本平均)







[1] 50.00111
[1] 0.6388567







##
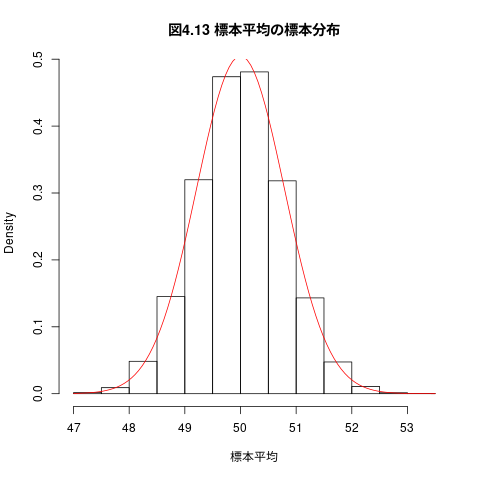
# png("graphs/fig-04-13.png", width=400, height=300)
##
hist(標本平均,freq=FALSE, main="図4.13 標本平均の標本分布")
curve(dnorm(x, mean=this.mean, sd=this.sd/sqrt(this.sample_size)), add=TRUE, col="red")









    

  • 図4.13 標本平均の標本分布
    

    


    

    04-13.png

    

    

    

    • 










4.5.5 不偏性





推定値 (e.g. 標本平均) の平均 (e.g. 標本分布の平均) は
母集団分布によらず，
母数 (e.g. 母平均) に一致すること





標本平均は，母平均の不偏推定量である。










4.5.6 標準誤差





推定量の標本分布を調べるときの2つの観点のうち「（2）標本分布が横
に大きく広がっていないか」にかかわるのが標準誤差です。





標準誤差は、推定量の標本分布の標準偏差と定義する





標準誤差が小さいということ



    

  • 運不運によって結果が大きく左右されない
    • 

  • また、誰がいつやってもだいたい同じ結果が安定
して得られる
    • 





上の \( N(50,10^2) \)の正規母集団から \( n=10 \) の標本を抽出した
ときの標本平均の例では、



    

  • 標本平均の標本分布はN(50,10)だったので，
    • 

  • 標準誤差は \( \sqrt{10} \) となります。
    • 





一般的に、



    

  • 母集団が，平均 \( \mu \)、分散\( \sigma^2 \) の正規分布で
    • 

  • 標本サイズ \( n \) の標本を抽出したとき、
    • 

  • その標本平均の標本分布は \( N(\mu, \frac{\sigma^2}{n}) \)となる
    • 

  • 標準誤差は \( \frac{\sigma}{\sqrt{n}} \) となる。
    • 





このことから、




    

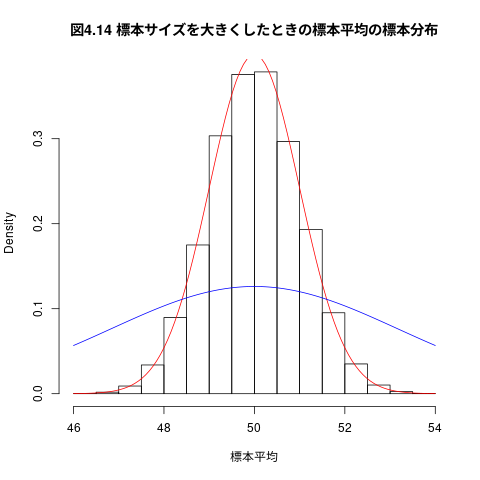
  1. 母集団分布の分散（標準偏差）が大きいほど、標本平均の標準誤差が
大きくなる。つまり、母分散が大きいと、そこから無作為抽出した標
本の平均値は母平均から外れた値をとりやすくなる。
    2. 


  2. 標本サイズが大きいほど、標本平均の標準誤差が小さくなる。つ
まり、標本サイズを大きくすれば、そこから無作為抽出した標本
の平均値は母平均に近い値をとりやすくなる
    3. 





実際に、先ほどの\( N(50,10^2) \) という母集団からの標本抽出の例で、標本サ
イズを10倍の \( n=100 \) にしてみると






this.sample_size <- 100
標本平均 <- numeric(length=this.counts)
      
for(i in 1:this.counts) {
  標本 <- rnorm(n=this.sample_size, mean=this.mean, sd=this.sd)
  標本平均[i] <- mean(標本)
}

mean(標本平均) ## 付加
var(標本平均)

誤差絶対値5以下 <- ifelse( abs(標本平均-50) <= 5, 1, 0) ## 付加
table(誤差絶対値5以下) ## 付加







[1] 50.01843
[1] 1.013532
誤差絶対値5以下
    1 
10000








##
## png(RforS-graphs/04-14.png)

hist(標本平均,freq=FALSE, main="図4.14 標本サイズを大きくしたときの標本平均の標本分布")
curve(dnorm(x,mean=50,sd=this.sd/sqrt(this.sample_size)),col="red",add=TRUE)
curve(dnorm(x,mean=50,sd=this.sd/sqrt(10)),col="blue",add=TRUE)










図4.14 標本サイズを大きくしたときの標本平均の標本分布






04-14.png

















4.6 標本分散と不偏分散の標本分布




    

  • 不偏分散は，母分散の不偏推定量
    • 

  • 
標本分散は，標本の散布度

    


    

    ##
## 4.6 標本分散と不偏分散の標本分布
##

samples.no <- 10000   # いくつ標本を用いるか
sample.size <- 10     # ひとつの標本の中のデータの個数

this.mean <- 50       # 分布の平均
this.sd <- 10         # 分布の標準偏差

標本分散s <- numeric(samples.no) # 各々の標本の分散値の保存場所
不偏分散s <- numeric(samples.no) # 各々の標本の不偏分散値の保存場所

for (i in 1:samples.no) {
  標本 <- rnorm(n=sample.size, mean=this.mean, sd=this.sd) # ひとつの標本の生成
  標本分散s[i] <- mean((標本-mean(標本))^2) 
  不偏分散s[i] <- var(標本)
}

c(mean(標本分散s),sd(標本分散s))  # 標本分散達の平均と分散
c(mean(不偏分散s),sd(不偏分散s))  # 標本不偏分散達の平均と分散

    

    • 




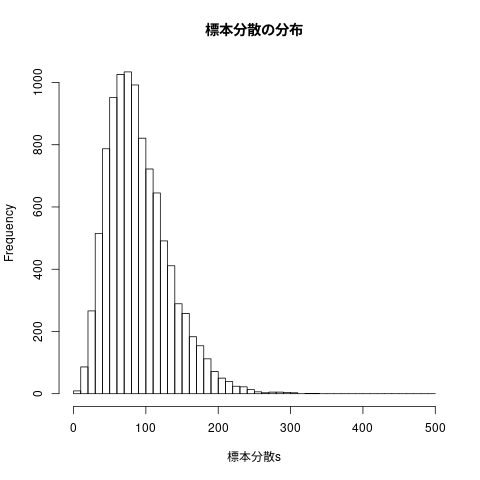
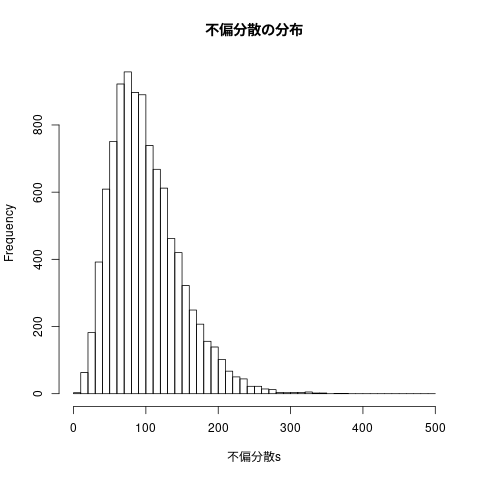
[1] 90.08901 42.72613
[1] 100.09890  47.47348







##
## 標本分散の頻度表
##
hist(標本分散s, breaks=seq(0,500,10), main="標本分散の分布")









##
## 標本不偏分散の頻度表
##
hist(不偏分散s, breaks=seq(0,500,10), main="不偏分散の分布")











図4.15 標本分散と不偏分散の分布





04-15-1.png 04-15-2.png







##
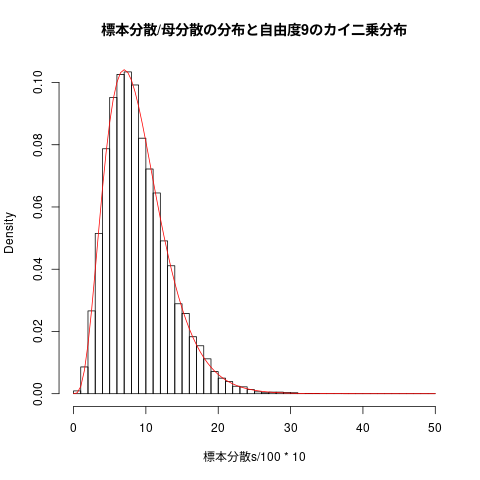
## 標本分散の分布
##
hist(標本分散s/100*10, freq=FALSE, breaks=seq(0,50,1), main="標本分散/母分散の分布と自由度9のカイ二乗分布")
curve(dchisq(x,9), add=TRUE, col="red")








##
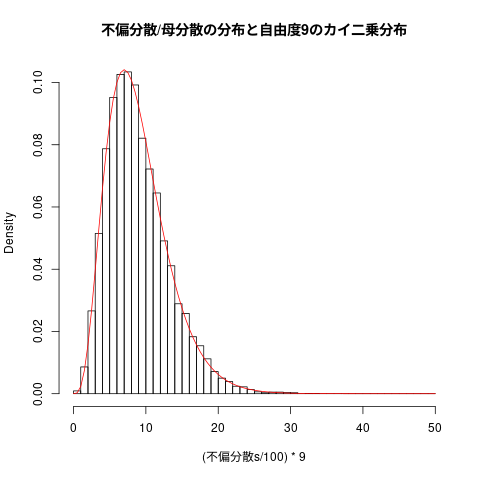
## 標本不偏分散の分布
##
hist((不偏分散s/100)*9, freq=FALSE, breaks=seq(0,50,1), main="不偏分散/母分散の分布と自由度9のカイ二乗分布")
curve(dchisq(x,9), add=TRUE, col="red")







04-15-3.png  04-15-4.png















Author: suzuki@iwate-u.ac.jp 鈴木正幸，非常勤講師


Created: 2021-12-01 水 20:50


Validate