RforS 4章 (データ解析)
Rによるやさしい統計学
rm -f RforS-Codes/04-*.R
4章 母集団と標本
4.1 母集団と標本
重要な用語
- 母集団
- 対象のデータ全体
- 標本
- 母集団から一部のデータを取り出した(抽出した)もの。 標本数を標本の大きさという。
- 標本抽出
- 母集団から一部のデータを取り出すこと
- 母数 (パラメーター)
- 母集団の性質をあらわす統計的指数(比率、平均、分散、相関係数など)
4.2 推測統計の分類
推測統計とは, 標本から母集団の性質を推し測ること
推定
点推定
標本から母数の値を求める
区間推定
標本から母数の値の範囲を求める
検定
- 母集団について述べた二つの異なる主張(仮説)
- どちらを採択するかを決める
4.3 点推定
手順
- 標本の抽出 標本のサイズ \( n \)
- 標本を用いて,母平均の推定値を計算する
#### ## 標本 身長 <- c(165.2, 175.9, 161.7, 174.2, 172.1, 163.3, 170.9, 170.6, 168.4, 171.3) ## 標本平均 mean(身長) ## 標本不偏分散 (後出) var(身長)
[1] 169.36 [1] 21.66711
意味
- 記述統計の文脈では,数値要約のための代表値を求める,こと
- 推測統計の文脈では,母平均の点推定を行う,こと
推定量と推定値
- 標本統計量
- 標本平均,標本分散,…
- 母集団の統計量
- 母平均,母分散,。。。
標本抽出に伴なう誤差
- 推定値と母数の誤差
4.4 推定値がどれくらいあてになるのかを調べる方法
rm -f RforS-Codes/04-04.R
4.4.1 単純無作為抽出
標本抽出の方法としての単純無作為抽出
4.4.2 確率変数
単純無作為抽出によって得られるデータの性質としての確率変数
4.4.3 確率分布
確率変数がどのような値をとるのかを示す確率分布
一様分布 (unif())
- サイコロ振りの実験 \( n=6 \)
## ## 一様分布に従う6個の標本の抽出 (サイコロ6 <- ceiling(runif(n=6,min=0,max=6))) ## 頻度表の作成 table(サイコロ6)
[1] 4 4 3 4 1 6 サイコロ6 1 3 4 6 1 1 3 1
- サイコロ振りの実験 \( n=60000 \)
## 一様分布に従う6000個の標本の抽出 サイコロ60000 <- ceiling(runif(n=60000,min=0,max=6 ) ## 頻度表の作成 # table(サイコロ60000)
4.4.4 母集団分布
確率分布を用いた母集団の表現としての母集団分布
(例) 男女比が 2:1 である母集団
## ## (例) 男女比が 2:1 である母集団 barplot(c(2/3, 1/3), names.arg=c("男性", "女性"), xlab="性別", ylab="比率", main="図4.3 性別の母集団分布の例") box(lty=1)
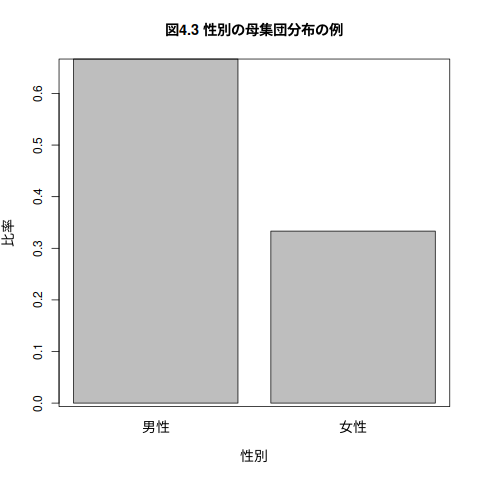

無作為抽出の標本は,母集団分布に従う
4.4.5. 代表的な母集団分布である正規分布
## ## 正規分布のグラフを描く ## png("graphs/norm_graphs.png",width=400,height=300) 出力を PNG形式のファイルへ curve(dnorm(x), from=-4, to=4, main="図4.4-5 正規分布 N(0, 1), N(0,2), N(1,1)") # 標準正規分布のグラフ, -4 から +4 の範囲 curve(dnorm(x,sd=2), add=TRUE) # 平均0, 偏差2 の正規分布,上描き curve(dnorm(x,mean=1,sd=1), add=TRUE) # 平均1, 偏差1 の正規分布,上描き
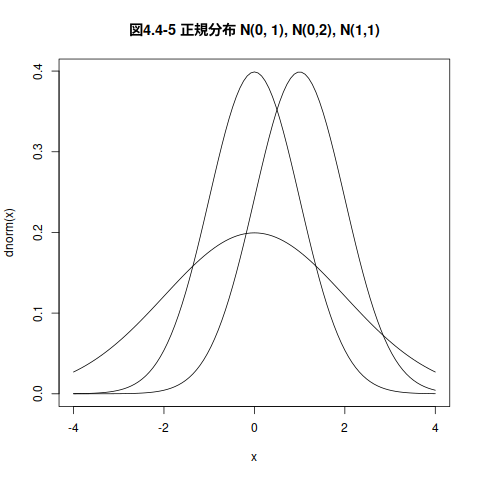

4.4.7 正規母集団から単純無作為抽出を行なう
Rを使って正規分布の母集団から標本を抽出する方法
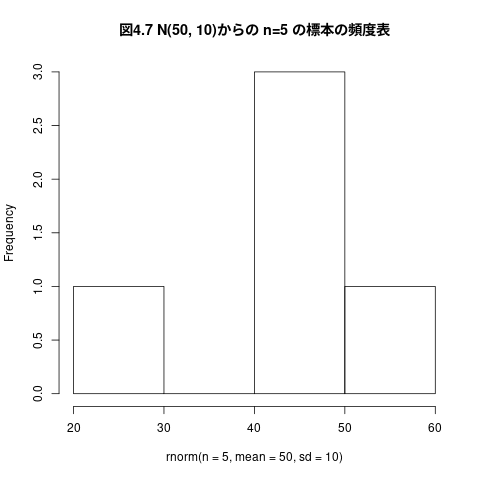
例えば、平均50、標準偏差10の正規母集団からn=5の標本を無作為抽出 する
## ## 平均50、標準偏差10の正規母集団からn=5の標本を無作為抽出する #### png("graphs/fig-04-07.png", width=400,height=300) rnorm(n=5, mean=50, sd=10) # 標本の抽出 hist(rnorm(n=5, mean=50, sd=10), main="図4.7 N(50, 10)からの n=5 の標本の頻度表") # 頻度表の描画
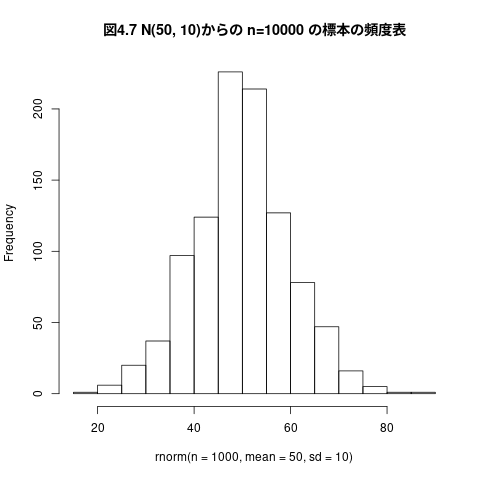
## ## 平均50、標準偏差10の正規母集団からn=1000の標本を無作為抽出する #### png("graphs/fig-04-08.png", width=400,height=300) hist(rnorm(n=1000, mean=50, sd=10), main="図4.8 N(50, 10)からの n=1000 の標本の頻度表")
4.5 標本分布
rm -f RforS-Codes/04-05.R
- 標本分布
- 標本統計量の確率分布のこと
- 推定値の信頼性の判断に用いる
- 標本における個々のデータの実現値を表した度数分布ではなく、
- 標本統計量の確率分布である
4.5.1 標本分布から何が分るのか
- 図4.9 標本分布の中心は、ほぼ「母数の本当の値」の ところに来ている
- 図4.10 標本分布の中心は、「母数の本当の値」からずれている
- 図4.11
- 標本分布の中心は、ほぼ「母数の本当の値」のところに来てい るが,
- 当たり外れが大きくて、推定値はあまりあてになるとはいえなそう
標本分布を調べるときの観点候補:
(1)標本分布が母数の本当の値を中心として分布しているか (2)標本分布が横に大きく広がっていないか
4.5.2 標本分布を経験的に求める
標本分布は次のものから数学的に求まる:
- 母集団分布
- 標本統計量の計算式 (変数変換)
- 標本数
Rを用いて,理論的ではなく,経験的の標本分布を求めることができる
標本統計量の実現値を大量に得られれば,そのヒストグラムは,標本分 布近いものとなるはず。
- サイズ \( n \) の標本を何度も繰かえし抽出し,実現量を計算し,ヒス トグラムを作成する
しかし,母集団分布が母数を含めてわかっていないため,
- 「もし母集団分布がこのような正規分布だったら、
- このくらいあてになる推定値が得られる」
ということを検討することになる。
4.5.3 正規母集団の母平均の推定
- 母集団分布 \( \sim N(50, 10^2)\)
- \( n = 10 \)
- 母平均の推定量は,標本平均 \( \overline{X} \)
## ## 標本サイズ10の標本による,母平均の推定 標本 <- rnorm(n=10, mean=50, sd=10) mean(標本)
44.9971134002593
4.5.4 標本分布を求める
母平均の推定を10000回繰り返し
## ## 母平均の推定 ### 母集団 N(50, 10^2) から ### 標本サイズ 10の標本の標本平均 ### 10000個の標本平均の頻度表を描く this.mean <- 50 this.sd <- 10 this.counts <- 10000 for (this.sample_size in c(10,20,40,80,160)) { 標本平均 <- numeric(length=this.counts) for(i in 1:this.counts) { 1 標本 <- rnorm(n=this.sample_size, mean=this.mean, sd=this.sd) 標本平均[i] <- mean(標本) } cat("sample_size=", this.sample_size, "mean=", mean(標本平均), "var=", var(標本平均), "\n") }
sample_size= 10 mean= 50.00768 var= 9.70614 sample_size= 20 mean= 49.97293 var= 4.901012 sample_size= 40 mean= 49.97277 var= 2.490787 sample_size= 80 mean= 49.99391 var= 1.249024 sample_size= 160 mean= 50.00111 var= 0.6388567
hist(標本平均,main="図4.12 標本抽出10,000回のときの標本平均の分布")
図4.12 標本抽出10,000回のときの標本平均の分布
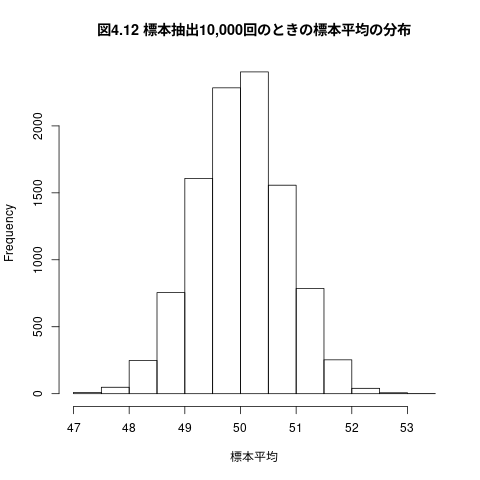
母平均 (50)からのズレが5以内か否かで振り分ける
## 母平均 (50)からのズレが5以内か否かで振り分ける 誤差絶対値5以下 <- ifelse( abs(標本平均-50) <= 5, 1, 0) table(誤差絶対値5以下)
| 0 | 1190 |
| 1 | 8810 |
88%くらいは,母平均+-5に収まっている
- (n → inf) で \( E(\overline{X}) = \)母平均
## ## 10000個の標本平均の平均値 mean(標本平均) ## 10000個の標本平均の分散値 var(標本平均)
[1] 50.00111 [1] 0.6388567
## # png("graphs/fig-04-13.png", width=400, height=300) ## hist(標本平均,freq=FALSE, main="図4.13 標本平均の標本分布") curve(dnorm(x, mean=this.mean, sd=this.sd/sqrt(this.sample_size)), add=TRUE, col="red")
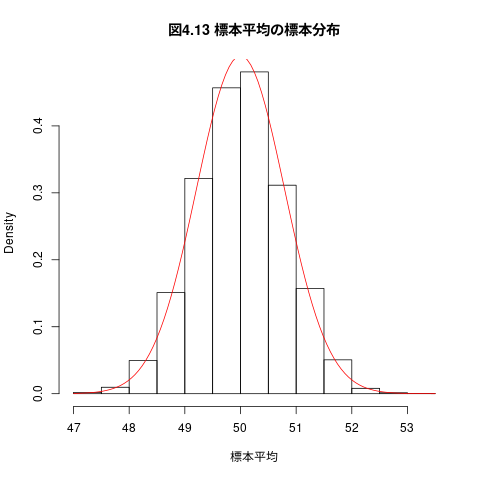
4.5.5 不偏性
推定値 (e.g. 標本平均) の平均 (e.g. 標本分布の平均) は 母集団分布によらず, 母数 (e.g. 母平均) に一致すること
標本平均は,母平均の不偏推定量である。
4.5.6 標準誤差
推定量の標本分布を調べるときの2つの観点のうち「(2)標本分布が横 に大きく広がっていないか」にかかわるのが標準誤差です。
標準誤差は、推定量の標本分布の標準偏差と定義する
標準誤差が小さいということ
- 運不運によって結果が大きく左右されない
- また、誰がいつやってもだいたい同じ結果が安定 して得られる
上の \( N(50,10^2) \)の正規母集団から \( n=10 \) の標本を抽出した ときの標本平均の例では、
- 標本平均の標本分布はN(50,10)だったので,
- 標準誤差は \( \sqrt{10} \) となります。
一般的に、
- 母集団が,平均 \( \mu \)、分散\( \sigma^2 \) の正規分布で
- 標本サイズ \( n \) の標本を抽出したとき、
- その標本平均の標本分布は \( N(\mu, \frac{\sigma^2}{n}) \)となる
- 標準誤差は \( \frac{\sigma}{\sqrt{n}} \) となる。
このことから、
- 母集団分布の分散(標準偏差)が大きいほど、標本平均の標準誤差が 大きくなる。つまり、母分散が大きいと、そこから無作為抽出した標 本の平均値は母平均から外れた値をとりやすくなる。
- 標本サイズが大きいほど、標本平均の標準誤差が小さくなる。つ まり、標本サイズを大きくすれば、そこから無作為抽出した標本 の平均値は母平均に近い値をとりやすくなる
実際に、先ほどの\( N(50,10^2) \) という母集団からの標本抽出の例で、標本サ イズを10倍の \( n=100 \) にしてみると
this.sample_size <- 100 標本平均 <- numeric(length=this.counts) for(i in 1:this.counts) { 標本 <- rnorm(n=this.sample_size, mean=this.mean, sd=this.sd) 標本平均[i] <- mean(標本) } mean(標本平均) ## 付加 var(標本平均) 誤差絶対値5以下 <- ifelse( abs(標本平均-50) <= 5, 1, 0) ## 付加 table(誤差絶対値5以下) ## 付加
[1] 50.01269
[1] 1.010955
誤差絶対値5以下
1
10000
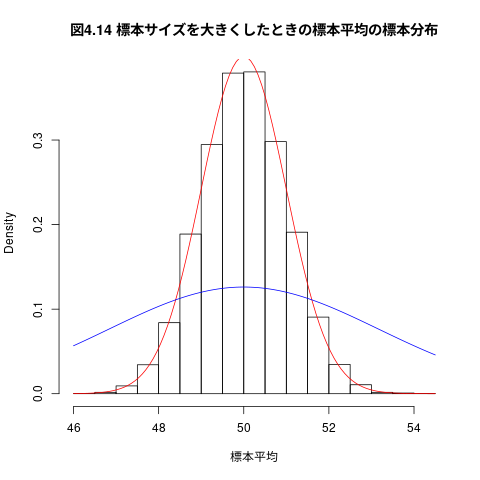
## ## png(RforS-graphs/04-14.png) hist(標本平均,freq=FALSE, main="図4.14 標本サイズを大きくしたときの標本平均の標本分布") curve(dnorm(x,mean=50,sd=this.sd/sqrt(this.sample_size)),col="red",add=TRUE) curve(dnorm(x,mean=50,sd=this.sd/sqrt(10)),col="blue",add=TRUE)
図4.14 標本サイズを大きくしたときの標本平均の標本分布
4.6 標本平均以外の標本分布
あらゆる標本統計量に対して標本分布を考えることができる。
標本分散と不偏分散の標本分布
- 不偏分散は,母分散の不偏推定量
- 標本分散は,標本の散布度
## ## 4.6 標本平均以外の標本分布 ## samples.no <- 10000 # いくつ標本を用いるか sample.size <- 10 # ひとつの標本の中のデータの個数 this.mean <- 50 # 分布の平均 this.sd <- 10 # 分布の標準偏差 標本分散s <- numeric(samples.no) # 各々の標本の分散値の保存場所 不偏分散s <- numeric(samples.no) # 各々の標本の不偏分散値の保存場所 for (i in 1:samples.no) { 標本 <- rnorm(n=sample.size, mean=this.mean, sd=this.sd) # ひとつの標本の生成 標本分散s[i] <- mean((標本-mean(標本))^2) 不偏分散s[i] <- var(標本) } c(mean(標本分散s),sd(標本分散s)) # 標本分散達の平均と分散 c(mean(不偏分散s),sd(不偏分散s)) # 標本不偏分散達の平均と分散
[1] 90.10345 42.49519 [1] 100.11495 47.21688
標本分散誤差100以上 <- ifelse(標本分散s>=100,1,0) 不偏分散誤差100以上 <- ifelse(不偏分散s>=100,1,0) table(標本分散誤差100以上) table(不偏分散誤差100以上)
標本分散誤差100以上 0 1 6512 3488 不偏分散誤差100以上 0 1 5585 4415
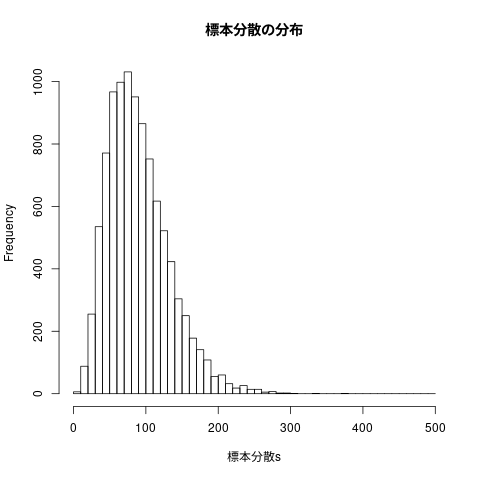
## ## 標本分散の頻度表 ## hist(標本分散s, breaks=seq(0,500,10), main="標本分散の分布")
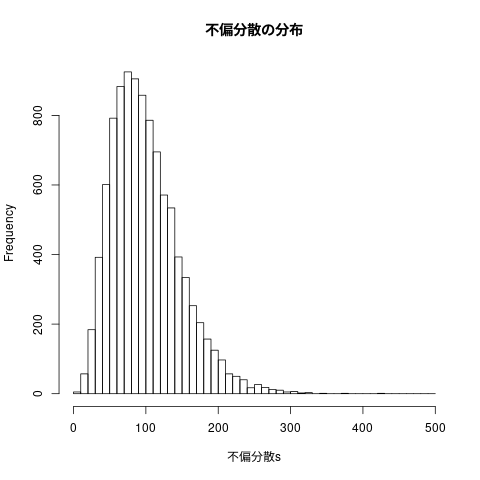
## ## 標本不偏分散の頻度表 ## hist(不偏分散s, breaks=seq(0,500,10), main="不偏分散の分布")
図4.15 標本分散と不偏分散の分布
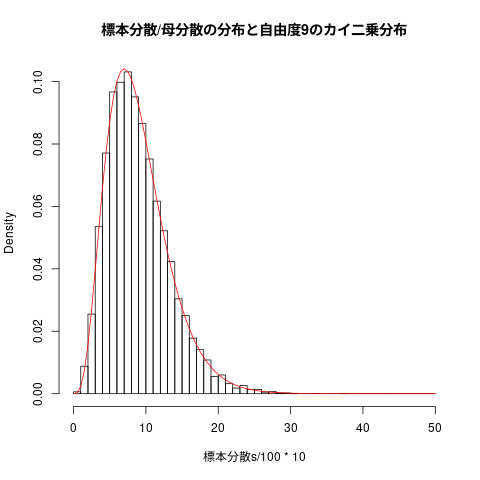
## ## 標本分散の頻度表 ## hist(標本分散s/100*10, freq=FALSE, breaks=seq(0,50,1), main="標本分散/母分散の分布と自由度9のカイ二乗分布") curve(dchisq(x,9), add=TRUE, col="red")
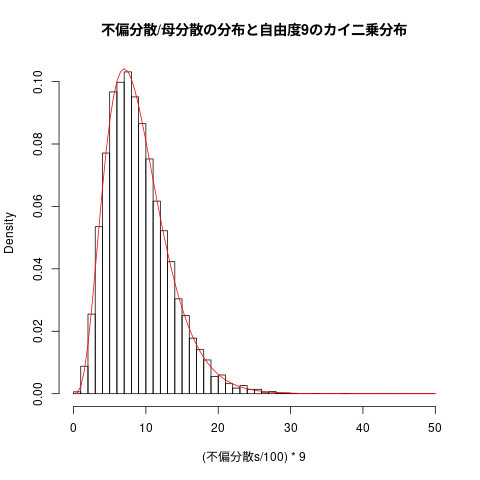
## ## 標本不偏分散の頻度表 ## hist((不偏分散s/100)*9, freq=FALSE, breaks=seq(0,50,1), main="不偏分散/母分散の分布と自由度9のカイ二乗分布") curve(dchisq(x,9), add=TRUE, col="red")


4.6.2 中央値の標本分布
母平均の推定量として,標本平均よりよい標本統計量はないのか?
- よい推定量
- 標本誤差の小さい推定値が得られやすい
中央値を母平均の推定量として使えるか
## ## 4.6.2 中央値を母平均の推定量として使えるか ## samples.no <- 10000 sample.size <- 10 this.mean <- 50 this.sd <- 10 標本平均s <- numeric(samples.no) 標本中央値s <- numeric(samples.no) for (i in 1:samples.no) { 標本 <- rnorm(n=sample.size,mean=this.mean,sd=this.sd) 標本平均s[i] <- mean(標本) 標本中央値s[i] <- median(標本) } c(mean(標本平均s), sd(標本平均s)) c(mean(標本中央値s), sd(標本中央値s))
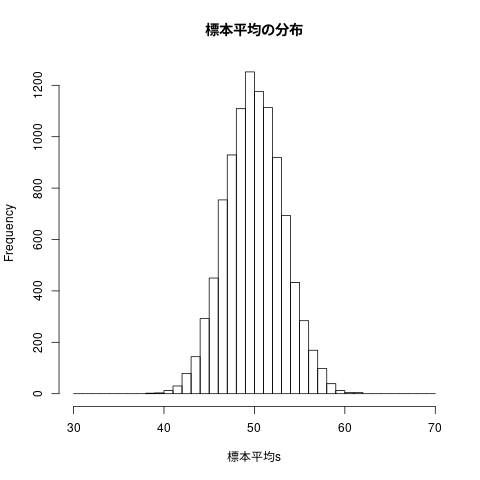
[1] 50.002369 3.183515 [1] 50.012799 3.748797
## ## 標本分散の頻度表 ## hist(標本平均s, breaks=seq(30,70,1), main="標本平均の分布")
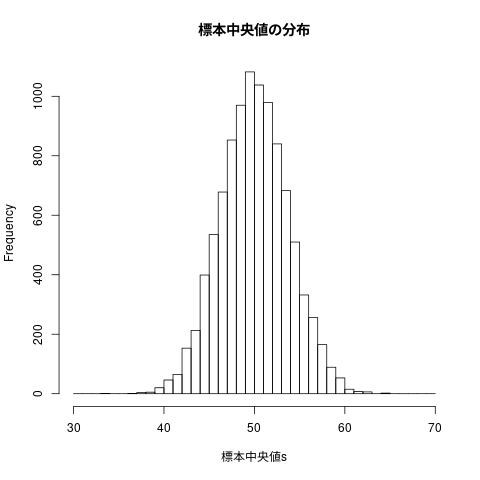
## ## 標本中央値の頻度表 ## hist(標本中央値s, breaks=seq(30,70,1), main="標本中央値の分布")