分散分析には、データの正規性や群間の分散の等質性が前提条件にあったり、分散分析後の事後テストがあったりなど、統計学に詳しくない人にとって、検定が正しく行われているのか判断が難しいことが多いです。

分散分析の実行方法では、それぞれの手順の具体例を与えて、プロットを交えながら、それぞれの検定の役割をみていきます。

分散分析の流れを次の図とステップに示します。

anova概要

• 分散分析は正規性の検定から始まります。

  正規性がない場合はノンパラメトリック手法で行います（ノンパラメト リック手法はこの記事では触れない）。

• 次に群間（グループ間）の分散等質性の検定を行う。

  比較したいグループ間の分散が同等であることを検定します。この条件 を満たしていれば次の分散分析が適用できます。分散の等質性が満たさ れない場合は、Welchの分散分析を適用します（分散が異なる場合はこ こでは触れない）。

• 分散分析（ANOVA）を行い、群間に差があるかを検定します。ここで、 有意な因子（グループを構成するもの、例：品種）が存在するならば、 次の事後テストを行います。有意な因子がない場合は、ここで検定を終 了し、グループ間に差異はないという結論を得ます。
• 最後に、有意であった因子に対して事後テストを行います。事後テスト を行うことでどの群間に差異があるのかを詳しく見ていきます。例えば、 品種A、B、Cに分散分析を行ったとき、分散分析では「品種のどれかの 間には違いがある」ということしか分かりません。事後テストでは品種 A、B、Cのうちどのペア（例AとB間、AとC間）に違いがあるのかを検証 することができます。

分散分析の流れは以上になります。

分散分析（ANOVA）やその検定のプロットを行う前提として各種パッケージをインストールする必要があります。

次を実行しパッケージのインストールを行い、ライブラリへの追加を行います。

install.packages("ggpubr")
install.packages("rstatix")
 
install.packages("ggplot2")
install.packages("gridExtra")
 
library(ggpubr)
library(rstatix)
 
library(ggplot2)
library(gridExtra)

ggpubrは分散分析のプロットに用います。

rstatixは分散分析や事後テストの検定を行うため、またその検定結果をプロット上に表示させるために用います。

これらのパッケージを用いて、次のirisのデータセットを例に分散分析を行っていきます。

class(iris)
head(iris)

[1] "data.frame"
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

まず分散分析の前提として、正規性の検定を行います。

今回irisのSepal.WidthのデータをSpeciesという因子に関して分散分析をします。

Sepal.Widthが正規性を持たない（母集団が正規分布でない）場合、分散分析を適用することができません。

そこでここで紹介する正規性の検定が必須となります。

統計ソフトRで正規分布の確認のため正規確率プロットを描くには？ - 統計ER

• 図で正規分布のチェック
  • qqnorm()を使う。
  • 正規確率プロットを描く。x軸が正規分布の論理的な分位数、y軸が実測値の分位数。
  • 対角線上にまっすぐに、プロットがならべば、正規分布していると判断できる。

次のコードを実行することで、正規性に関するプロット及び正規性の検定を行 うことができます。

#正規性の確認
qqnorm(iris$Sepal.Width ,ylab = "wid")
qqline(iris$Sepal.Width)
 
shapiro_test <- shapiro.test(t(iris$Sepal.Width))

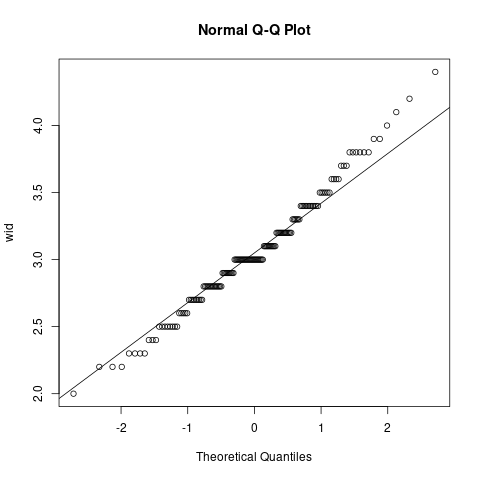
• y=xの対角線上にデータのプロットが集中しているほど、データが正規性を持つことがいえます。
• 上の場合、Sepal.Widthは正規性をもっていることがうかがえます。

• プロットだけでは判断できない場合も、5行目を実行することで、正規性の 検定であるシャピロ・ウィルク検定を行うことができます。

  p値が0.05より大きい場合は正規性をもつことがいえて、次のステップに進 むことができます。

  ここで、p値が0.05以下の場合は、クリスカルウォリス検定などの分散分析 のノンパラメトリック手法を検討する必要があります。

実際に次を実行すると、Sepal.Widthに関するシャピロ・ウィルク検定のp値は0.1012>0.05であり、正規性があることが分かりました。 a