確率と統計 7.標本と統計的推測
標本平均の性質
標本平均
- 記法
- \( \overline{X_{(n)}} \), \( (n) \)は標本サイズを表わすこの文書での 記法
- 意味
- \( \overline{X_{(n)}} = \Sigma_{1}^{n} X_i/n \), \( X_{i=1:n} \) は 母集団 \( X \) からの 標本
- 関連
- 確率変数の和の,平均,分散,確率分布
標本平均は \( \mu \) に 確率収束 する – 一致性,大数の法則
\( \overline{X_{(n)}} \stackrel{P}{\longrightarrow} \mu\) \( (n \longrightarrow \infty) \)
標本平均 は, 母平均 \( \mu \) に 確率収束 する
標本平均の期待値は \( \mu \) – 不偏性
確率変数の和の平均の期待値の公式より,
\( \rm{E}(\overline{X_{(n)}}) = \mu \)
標本平均の分散
(確率変数の和)の分散の期待値の公式より,
\( \rm{E}(S^{2}_{(n)}) = \sigma^2 / {n} \)
標本平均が従がう分布は
\( \rm{N}(\mu, \sigma^2/n) \)
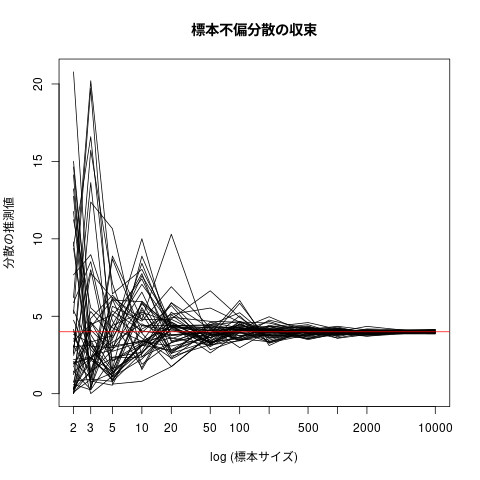
標本不偏分散の性質
標本不偏分散
標本不偏分散 \( S_{n}^2 = \Sigma_{i=1}^{n} (X_i - \bar{X_{n}})^2 / (n-1) \)
(分散の) 推定量 の計算式中に, 別 (平均)の推定量を含んでいる。
この計算式(標本不偏分散)は,独立な,(n-1)変数の関数になる。この個数 を 自由度 と呼ぶ。
\( \overline{X_{(n)}} = \Sigma_{1}^{n} X_i/n \) が制限として加わることにな る。
一致性
\( S_{n}^2 \longrightarrow \sigma^2\) \( (n \longrightarrow \infty) \)
不偏性
\( \rm{E}[S_{n}^{2}] = \sigma^{2} \)
標本不偏分散が従う標本分布
\( (n-1) S_{n}^2 / \sigma^2 \sim \chi^{2} \)
理由
\begin{eqnarray} (n-1) S_{n}^{2} & = & \Sigma_{i=1}^{n} (X_i^2 - \bar{X}_n)^2) \\ & = & \Sigma_{i=1}^{n}X_i^2 - n \bar{X}_n^2 \\ & = & \vec{X}^t \vec{X} - n \vec{\bar{X}_n}^t \vec{\bar{X}_n} \\ & = & {X}^2 - n {\bar{X}_n}^2 \\ \end{eqnarray}
次節の説明より, 自由度 \( (n-1) \)のカイ二乗分布に従う。
\[ \frac{(n-1) S_{n}^{2}}{\sigma^2} \sim \chi^2_{n-1} \]
標本平均と標本不偏分散の独立性,および標本不偏分散が従う標本分布
変数変換行列 \(A\)
次の変数変換を考える: (標本平均を独立変数として見るため)
\begin{eqnarray} Y_1 & = & \sqrt{n} \overline{X_{(n)}} = \Sigma_{i=1}^n X_i /\sqrt{n}\\ Y_2 & = & (X_1- X_2)/\sqrt{2} \\ Y_3 & = & (X_1 + X_2 - 2 X_3)/\sqrt{2\cdot3} \\ \cdots & = & \cdots \\ Y_n & = & (\Sigma_{i=1}^{n-1}X_i - (n-1) X_n)/\sqrt{n\cdot(n-1)} \end{eqnarray}上記の変換を,変換行列 \( A \)で記述する:
\( \vec{Y} = A \vec{X} \)
\begin{eqnarray} \vec{X} & = & (X_1, X_2, \cdots, X_n)^t \\ \vec{Y} & = & (Y_1, Y_2, \cdots, Y_n)^t \\ %% \vec{j} & = & (1, 1, \cdots, 1)^t \\ %% \vec{a} & = & \vec{j}/\sqrt{n} \\ %% & = & (1/\sqrt{n} , \cdots, 1/\sqrt{n})^t \\ \end{eqnarray} \begin{equation} A = \left( \begin{array}{ccccc} 1/\sqrt{n} & 1/\sqrt{n} & 1/\sqrt{n} & \cdots & 1/\sqrt{n} \\ 1/\sqrt{2} & -1/\sqrt{2} & 0 & \cdots & 0 \\ 1/\sqrt{6} & 1/\sqrt{6} & -2/\sqrt{6} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & 0 \\ \frac{1}{\sqrt{n\cdot(n-1)}} & \frac{1}{\sqrt{n\cdot(n-1)}} & \frac{1}{\sqrt{n\cdot(n-1)}} & \cdots & - \frac{(n-1)}{\sqrt{n\cdot(n-1)}} \end{array} \right) \end{equation}変換A, A^t は直交変換
\( A^t A = A A^t = E \)は容易に確かめられる。 すると,\(A^t=A^{-1}\)となる。
このような性質を持つ行列は,直交行列と呼ばれる。
逆変数変換 \( \vec{Y} = A^t \vec{X} \)
\( \vec{Y} = A \vec{X} \), \( \vec{X} = (X_1, X_2, \cdots, X_n) \) のとき,
\(A^{-1} = A^t \)なので,\( \vec{Y} = A^t \vec{X} \)
\( Y_1 \) と \( Y_{i=2:n} \) は独立
\( A_{i=1:n} \) を,行列 \( A \) の i 行目の横ベクトルとする。
\begin{equation} A = \left( \begin{array}{c} \vec{A_1}\\ \vec{A_2}\\ \cdots\\ \vec{A_n}\\ \end{array} \right) \end{equation}行列\( A^t \)を横ベクトルを縦に並べたものと解釈するということ。
\begin{eqnarray} \vec{A^t_1} \vec{A_1}^t & = & 1 \\ \vec{A^t_1} A_{i=2:n}^t & = & 0 \\ \vec{A^t_{i=2:n}} \vec{A_{j=2:n}} & = & \delta_{ij} \\ \end{eqnarray}つまり,\(A\) の基底ベクトルは全て直交し長さ1,\(A\)の階数は\(n\)で,線形独立な \( \vec{X} \) は, 互いに独立な,ベクトル \( \vec{Y} = (Y_1, \cdots. Y_n)^t \) に変換される。
\( (\vec{X}^t \vec{X} - n \overline{X_{(n)}}^2) \sim \chi^2(n-1) \)
\[ Y_1 = \vec{A^t_1} \vec{X} = \Sigma_{i=1}^{n} X_i /\sqrt{n} \]
\begin{eqnarray} Y_1^2 & = & (\vec{A^t_1} \vec{X})^t (\vec{A^t_1} \vec{X})\\ & = & (\Sigma_{i=1}^{n} X_i /\sqrt{n})^2 \\ & = & n \overline{X_{(n)}}^2 \\ \end{eqnarray} \begin{eqnarray} \vec{X}^t \vec{X} - n \overline{X_{(n)}}^2 & = & (A^{t}Y)^t A^{t}Y - Y_1^2 \\ & = & Y_2^2 + \cdots + Y_n^2 \\ \end{eqnarray}\[ Y_{i=2:n} \sim N(0, \sigma^2) なので Y_{i=2:n}/\sigma \sim N(0,1) \]
標本分散の標本分布
\( (n-1) S^2 = Y_2^2 + Y_3^2 + \cdots + Y_n^2 \) であるので,
\( \frac{(n-1) S^2}{\sigma^2} = (Y_2/\sigma)^2 + (Y_3/\sigma)^2 + \cdots (Y_n/\sigma)^2) \) である。
\( Y_{i=2:n} \sim N(0, \sigma^2) \) なので,
\( Y_{i=2:n}/\sigma \sim N(0, 1) \).
なので,\( \frac{(n-1) S^2}{\sigma^2} \) は 自由度 \( n-1 \) のカイ二乗分布にしたがう。
大数の法則と中心極限定理
確率収束
確率変数 \(X_n\) が 確率変数 \(X\)に確率収束する
- 記法
- \( X_n \stackrel{P}{\longrightarrow} X \)
- 意味
- \( \forall \epsilon \lim_{n \rightarrow \infty} P(|X_n - X| > \epsilon) = 0 \)
大数の法則
標本数が大きくなると,統計値は一定の値に近づく (確率収束)
\( \overline{X_{(n)}} \stackrel{P}{\longrightarrow} \mu \)
\(\overline{S^2_{(n)}} \stackrel{P}{\longrightarrow} \sigma^2 \)
中心極限定理
確率変数の和の分布は,変数の数が多くなると,正規分布に近づく (分布 収束)
\( \lim_{n\rightarrow\infty} \overline{X_{(n)}} \sim N(\mu, \sigma^2/n) \)
\( B(n,p) \stackrel{P}{\longrightarrow} N(np, np(1-p)) \) \( (n\rightarrow \infty) \)
標準化とスチューデント化
確率変数 \( X \sim N(\mu, \sigma^2)\) の標準化 \( Z = \frac{X-\mu}{\sigma} \sim N(0,1) \)
\( \overline{X_{(n)}}\) の標準化
母分散既知の場合の母平均の推定に用いる:
\(Z_n = \frac{\overline{X_{(n)}}-\mu}{\sigma/\sqrt{n}} \sim N(0,1) \)
\( \overline{X_{(n)}}\) のスチューデン化
母分散が未知の場合の母平均の推定に用いる:
\(T_n = \frac{\overline{X_{(n)}}-\mu}{\sqrt{S^2/n}} ~ \sim t_{n-1}\)
確率分布 t-分布 \( t_{n-1} \)
t-分布は,\( n\rightarrow\infty \) で, 標準正規分布に, 分布収束 する。
\( t_{n-1} \stackrel{d}{\longrightarrow} N(0,1) \)
母分布が未知の場合
大標本であれば,
\( t_{n-1} \stackrel{d}{\longrightarrow} N(0,1) \) をもちいて,
\(T_n = \frac{\overline{X_{(n)}}-\mu}{\sqrt{S^2/n}} ~ \sim N(0,1)\)
標本が従う分布
- \( \chi^2 \) 分布
- データの平方和である統計量 \( \chi^2 \) が従う分布
- 母分散の区間推定
- 独立性の検定
- \( F \) 分布
- 二つの \( \chi^2 \) の比が従う分布
- 等分散の検定
- 分散分析
\(\chi^2\)-分布 標本不偏分散
t-分布 チューデント化
F-分布 標本不偏分散の比
\( \chi^2 \) 分布
工場で製造される製品の容量のバラツキは?
データの平方和
標準正規母集団からの無作為標本
\( X_{i=1:n} \) 標準正規母集団からの無作為標本
- 母集団が正規分布の場合は,標準化する
\( \chi^2 \) 統計量
標準化
\( X ~ N(\mu, \sigma^2) \) のとき, \( Z = \frac{X-\mu}{\sigma} \) \( \sim N(0, 1) \) となる。
\( Z^2 \) は,\(E[Z^2] = 0 \), \(V[Z^2]=2\), \( Z^2 \sim \chi^2_{(1)} \) (自由度1のカイ二乗分布) となる。
標準化された平方和の分布
\( \chi^2_{(n)} = \Sigma_{i=1}^{n} Z_i^2 = \Sigma_{i=1}^{n} (X_i-\mu)^2/\sigma^2 \)
自由度1のカイ二乗分布の和であるので,
- \( n \) は自由度。
- 期待値は \( n \),
- 分散は, \( 2 n \)
- 再生成 \( \chi^2_{(m+n)} = \chi^2_{(m)} + \chi^2_{(n)} \)
\( \chi^2 \) 分布
- 非対称, 平均は中央にない
curve(dchisq(x,df=1),from=0, to=10, lty=1, col=1,main="自由度によって形が変るカイ二乗分布") curve(dchisq(x,df=3),from=0, to=10, lty=1, col=2, add=T) curve(dchisq(x,df=10),from=0, to=10, lty=1, col=3, add=T) legend(2, 0.7, c("自由度=1", "自由度=3", "自由度=10"), lty=c(1,1,1), col=c(1,2,3))

 (
(