7章 分散分析
7.0 分散分析 (anova, Analysis Of Variance)
3つ以上の 平均値を比較する ために,分散分析を紹介する
- 分散分析の考え方の基礎,「平方和の分解」
- 要因の数の違い,
- 標本の対応の有無による違い,がある
変動の区別
全体の変動
- 全データをまとめて扱う
- 全平均 と 個々のデータの偏差,分散
方法 (要因) の違いによる変動
- 方法ごとにグループを作成
- 全平均 と グループ内平均との偏差,分散
- 同じ方法で処方レベルの違い
個の違いによる変動 (誤差)
- 同じ方法グループ内のデータの変動は,個々の違いが原因。
- 方法の効果を見るためには,雑音と考える。
分散分析
全体の変動 = 方法 (要因)による変動 + 個の違いによる変動 となる。
要因毎にわけ,誤差に較べて大きな影響を与えている要因を探す。
7.1 一元配置分散分析
一つの要因の分析を行なう。
指導法データの準備
(指導法データ <- read.csv("data/shidouhouU8.csv")) class(指導法データ) str(指導法データ)
SID name sex math stat psych_test stat_test1 stat_test2 method 1 1 大村 男 嫌い 好き 13 6 10 C 2 2 本多 男 嫌い 好き 14 10 13 B 3 3 川崎 男 好き 好き 7 6 8 B 4 4 多村 男 好き 好き 12 10 15 A 5 5 松中 男 嫌い 嫌い 10 5 8 B 6 6 小久保 男 嫌い 嫌い 6 3 6 C 7 7 柴原 男 嫌い 嫌い 8 5 9 A 8 8 井手 男 嫌い 嫌い 15 9 10 D 9 9 田上 男 嫌い 嫌い 4 3 7 D 10 10 松田 男 好き 嫌い 14 3 3 D 11 11 高谷 女 好き 好き 9 11 18 A 12 12 杉内 女 嫌い 好き 6 6 14 A 13 13 和田 女 好き 好き 10 11 18 A 14 14 新垣 女 嫌い 嫌い 12 9 11 C 15 15 大隣 女 嫌い 好き 5 7 12 B 16 16 水田 女 好き 嫌い 12 5 5 D 17 17 斉藤 女 嫌い 嫌い 8 8 7 C 18 18 柳瀬 女 嫌い 嫌い 8 7 12 C 19 19 佐藤 女 嫌い 嫌い 12 7 7 B 20 20 馬原 女 嫌い 嫌い 15 9 7 D [1] "data.frame" 'data.frame': 20 obs. of 9 variables: $ SID : int 1 2 3 4 5 6 7 8 9 10 ... $ name : Factor w/ 20 levels "井手","高谷",..: 14 18 12 13 6 5 4 1 16 7 ... $ sex : Factor w/ 2 levels "女","男": 2 2 2 2 2 2 2 2 2 2 ... $ math : Factor w/ 2 levels "嫌い","好き": 1 1 2 2 1 1 1 1 1 2 ... $ stat : Factor w/ 2 levels "嫌い","好き": 2 2 2 2 1 1 1 1 1 1 ... $ psych_test: int 13 14 7 12 10 6 8 15 4 14 ... $ stat_test1: int 6 10 6 10 5 3 5 9 3 3 ... $ stat_test2: int 10 13 8 15 8 6 9 10 7 3 ... $ method : Factor w/ 4 levels "A","B","C","D": 3 2 2 1 2 3 1 4 4 4 ...
(As <- subset(指導法データ, method=="A")$stat_test2) (Bs <- subset(指導法データ, method=="B")$stat_test2) (Cs <- subset(指導法データ, method=="C")$stat_test2) (Ds <- subset(指導法データ, method=="D")$stat_test2) (統計テスト2 <- c(As, Bs, Cs, Ds)) (指導法 <- c(rep("A",5),rep("B",5),rep("C",5),rep("D",5))) (指導法2 <- factor(指導法)) # 要因型ベクトルに変換
[1] 15 9 18 14 18 [1] 13 8 8 12 7 [1] 10 6 11 7 12 [1] 10 7 3 5 7 [1] 15 9 18 14 18 13 8 8 12 7 10 6 11 7 12 10 7 3 5 7 [1] "A" "A" "A" "A" "A" "B" "B" "B" "B" "B" "C" "C" "C" "C" "C" "D" "D" "D" "D" [20] "D" [1] A A A A A B B B B B C C C C C D D D D D Levels: A B C D
指導法を受けている全ての人を母集団とし,その母集団において,指導法ごと に求めたテスト得点の平均値に違いがあるかを知りたい。
この20人のデータは,母集団からの無作為抽出標本です。
この標本が,母平均の等しい4群 (A,B,C,Dの指導法ごとの) から抽出された可 能性が高いかを検討する。
そのための検定が,*分散分析* です。
検定の流れ
帰無仮説と対立仮説の設定
- 帰無仮説 \(H_0\)
- 4群の母平均は等しい
- 対立仮説 \(H_2\)
- 4群の母平均は等しくない
検定統計量
\( F = \frac { \mbox{群間平方和} / \mbox{群間の自由度} } { \mbox{群内平方和} / \mbox{群内の自由度} } \)
\( F \) は,全ての群の母平均が等しいときに,* F分布 * に従う
- 群間平方和
- 全体平均値と群間平均値の差の2乗和, 自由度 (4ー1)
- 群内平方和
- 群内平均値との差の2乗和, 自由度 4*(5ー1)
F-分布の確率密度関数
curve(df(x, 3, 16),0, 5)
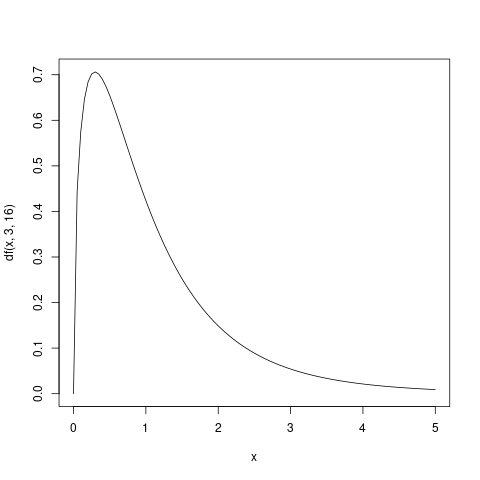
有意水準 \(\alpha\) の決定
\( \alpha=0.05 \) の片側検定, F値は正値。
統計検定量の実現値の計算
- oneway.test 関数
一元配置分散分析のみ実行可能
# var.equal=TRUEにより母分散の等質性を仮定 oneway.test(統計テスト2 ~ 指導法2, var.equal=TRUE )
One-way analysis of means data: 統計テスト2 and 指導法2 F = 7.1111, num df = 3, denom df = 16, p-value = 0.002988
p-値が,0.002988 であるので,帰無仮説を棄却。
- aov 関数
最も一般的
aov(統計テスト2 ~ 指導法2)
Call: aov(formula = 統計テスト2 ~ 指導法2) Terms: 指導法2 Residuals Sum of Squares 184 138 Deg. of Freedom 3 16 Residual standard error: 2.936835 Estimated effects may be unbalancedsummary(aov(統計テスト2 ~ 指導法2))
One-way analysis of means data: 統計テスト2 and 指導法2 F = 7.1111, num df = 3, denom df = 16, p-value = 0.002988
p-値が,0.002988 であるので,帰無仮説を棄却。
- anova関数
複数のモデルの比較など,高度な分析に対応
anova(lm(統計テスト2 ~ 指導法2))
Analysis of Variance Table Response: 統計テスト2 Df Sum Sq Mean Sq F value Pr(>F) 指導法2 3 184 61.333 7.1111 0.002988 ** Residuals 16 138 8.625 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1p-値が,0.002988 であるので,帰無仮説を棄却。
Rによる変動と検定値の計算
(全データ <- cbind(As, Bs, Cs, Ds))
As Bs Cs Ds
[1,] 15 13 10 10
[2,] 9 8 6 7
[3,] 18 8 11 3
[4,] 14 12 7 5
[5,] 18 7 12 7
(群平均 <- colMeans(全データ)) # 水準ごとの平均のベクトル
As Bs Cs Ds 14.8 9.6 9.2 6.4
# 水準ごとの平均のベクトルを行数だけ並べた行列を作る (群平均行列 <- matrix(rep(群平均, nrow(全データ)), nrow=nrow(全データ), ncol=ncol(全データ),byrow=TRUE))
[,1] [,2] [,3] [,4]
[1,] 14.8 9.6 9.2 6.4
[2,] 14.8 9.6 9.2 6.4
[3,] 14.8 9.6 9.2 6.4
[4,] 14.8 9.6 9.2 6.4
[5,] 14.8 9.6 9.2 6.4
(群間 <- 群平均行列 - mean(全データ))
[,1] [,2] [,3] [,4]
[1,] 4.8 -0.4 -0.8 -3.6
[2,] 4.8 -0.4 -0.8 -3.6
[3,] 4.8 -0.4 -0.8 -3.6
[4,] 4.8 -0.4 -0.8 -3.6
[5,] 4.8 -0.4 -0.8 -3.6
(群内 <- 全データ - 群平均行列) # 各データと、その群内の平均との差
As Bs Cs Ds
[1,] 0.2 3.4 0.8 3.6
[2,] -5.8 -1.6 -3.2 0.6
[3,] 3.2 -1.6 1.8 -3.4
[4,] -0.8 2.4 -2.2 -1.4
[5,] 3.2 -2.6 2.8 0.6
(群内平方和 <- sum(群内^2)) # 群内平方和
[1] 138
(群間平方和 <- sum(群間^2)) # 群内平方和
[1] 184
分母 <- 群内平方和 / ( (nrow(全データ)-1)*ncol(全データ) )
全体差
(全体差 <- 全データ - 全平均) # 行列 - スカラ
As Bs Cs Ds
[1,] 5 3 0 0
[2,] -1 -2 -4 -3
[3,] 8 -2 1 -7
[4,] 4 2 -3 -5
[5,] 8 -3 2 -3
群間差
群平均行列 から 全平均を引く
(群間差 <- 群平均行列 - 全平均)
[,1] [,2] [,3] [,4]
[1,] 4.8 -0.4 -0.8 -3.6
[2,] 4.8 -0.4 -0.8 -3.6
[3,] 4.8 -0.4 -0.8 -3.6
[4,] 4.8 -0.4 -0.8 -3.6
[5,] 4.8 -0.4 -0.8 -3.6
群内差
全データから各群内平均を引く
(群内差 <- 全データ - 群平均行列)
As Bs Cs Ds
[1,] 0.2 3.4 0.8 3.6
[2,] -5.8 -1.6 -3.2 0.6
[3,] 3.2 -1.6 1.8 -3.4
[4,] -0.8 2.4 -2.2 -1.4
[5,] 3.2 -2.6 2.8 0.6
平方
全体差^2 群間差^2 群内差^2
As Bs Cs Ds
[1,] 25 9 0 0
[2,] 1 4 16 9
[3,] 64 4 1 49
[4,] 16 4 9 25
[5,] 64 9 4 9
[,1] [,2] [,3] [,4]
[1,] 23.04 0.16 0.64 12.96
[2,] 23.04 0.16 0.64 12.96
[3,] 23.04 0.16 0.64 12.96
[4,] 23.04 0.16 0.64 12.96
[5,] 23.04 0.16 0.64 12.96
As Bs Cs Ds
[1,] 0.04 11.56 0.64 12.96
[2,] 33.64 2.56 10.24 0.36
[3,] 10.24 2.56 3.24 11.56
[4,] 0.64 5.76 4.84 1.96
[5,] 10.24 6.76 7.84 0.36
平方和と自由度とF-値
群間平方和 <- sum(群間^2) 群内平方和 <- sum(群内^2) 全体平方和 <- 群間平方和 + 群内平方和 (群間自由度 <- ncol(全データ)-1) (群内自由度 <- (nrow(全データ)-1) * ncol(全データ)) (全体自由度 <- length(全データ)-1 ) 全体自由度 - 群間自由度 - 群内自由度 (群間平均平方 <- 群間平方和/群間自由度) (群内平均平方 <- 群内平方和/群内自由度) (全体平均平方 <- 全体平方和/全体自由度) (F <- 群間平均平方 / 群内平均平方)
[1] 3 [1] 16 [1] 19 [1] 0 [1] 61.33333 [1] 8.625 [1] 16.94737 [1] 7.111111
7.1.3 多重比較 (Tukey の方法)
7.1.1項の帰無仮説の棄却では,4つの群の母平均が等しくないことは分 るが,どの群に間に差があるのかは分らない。
どの群に間に差があるのかを調べるために,* 多重比較 * とよばれる方 法を使う。
ここでは,Tukeyの方法について説明する。
検定統計量 q
各群のデータ数と分散が等しいと仮定します。
\[ q = \frac { | \textrm{比較する群の平均値差} | } { \sqrt{\textrm{群内の平均平方} / \textrm{各群のデータ数} }} \]
((s-:)) q は t-検定(分散が同じ2群の平均値の差の検定)に似ている
データの準備
指導法データ <- read.csv("data/shidouhouU8.csv")
(As <- subset(指導法データ, method=="A")$stat_test2)
(Bs <- subset(指導法データ, method=="B")$stat_test2)
(Cs <- subset(指導法データ, method=="C")$stat_test2)
(Ds <- subset(指導法データ, method=="D")$stat_test2)
(全データ <- cbind(As, Bs, Cs, Ds))
(指導法 <- 指導法データ$method)
# (指導法2 <- factor(指導法)) # 要因ベクトルに変換,違いがないような。。。
(統計テスト2 <- 指導法データ$stat_test2)
統計検定値 q の実現値値
(q <- abs(mean(As)-mean(Ds)) / sqrt(群内平均平方/nrow(全データ)))
[1] 6.395651
棄却域の決定
有意水準 5%, 平均値の数 4, 群内自由度 16,を指定します。
qtukey(0.95, 4, 16)
qtukey(0.05, 4, 16, lower.tail=FALSE)
[1] 4.046093 [1] 4.046093
どちらも4.046093となり,棄却域は \( q > 4.046093 \) となります。
TukeyHSD (Honest Significant Difference)
TukeyHSD(aov(統計テスト2 ~ 指導法))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = 統計テスト2 ~ 指導法)
$指導法
diff lwr upr p adj
B-A -5.2 -10.514108 0.1141085 0.0562227
C-A -5.6 -10.914108 -0.2858915 0.0371222
D-A -8.4 -13.714108 -3.0858915 0.0017736
C-B -0.4 -5.714108 4.9141085 0.9963241
D-B -3.2 -8.514108 2.1141085 0.3446966
D-C -2.8 -8.114108 2.5141085 0.4561325
7.2 一元配置分散分析 (対応あり)
一元配置分散分析 (対応あり)では、
- 同じ被験者が
- 複数の条件を経験する
などの対応のあるデータを対象とする。
例題
以下の表は5名の学生に、線形代数、微分積分、確率統計に対する好意度 の評定データである。 これら3つの科目に対する好意度に差があるだろ うか?(念のため:これは1要因3水準)
| 学生 | 線形代数 | 微分積分 | 確率統計 |
|---|---|---|---|
| 田中 | 7 | 5 | 8 |
| 岸 | 8 | 4 | 6 |
| 大引 | 9 | 7 | 7 |
| 吉川 | 5 | 1 | 2 |
| 荻野 | 6 | 3 | 5 |
対応がないものとして分散分析してみる
仮説
- 帰無仮説 H_0
- 3科目の好感度の母平均は等しい
- 対立仮説 H_1
- 3科目の好感度の母平均は等しくない
検定統計量 F ::
\[ F = \frac { \mbox{群間平方和} / \mbox{群間の自由度} } { \mbox{群内平方和} / \mbox{群内の自由度} } \]
\( F \) は,全ての群の母平均が等しいときに,* F分布 * に従う
- 群間平方和
- 全体平均値と群間平均値の差の2乗和
- 群内平方和
- 群内平均値との差の2乗和
対応がないものとして実行
好意度 <- c(7,8,9,5,6,5,4,7,1,3,8,6,7,2,5) 科目 <- factor(c(rep("線形代数",5),rep("微分積分",5),rep("確率統計",5))) summary(aov(好意度~科目)) # 好意度を科目の観点から分析する
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 2.641 0.112
Residuals 12 51.20 4.267
結果
- F値
- 2.641
- p値
- 0.1121 > 0.05
p値か 5%水準より大きいため, 有意な差は認められない。 帰無仮説を採択。
7.2.2 一元配置分散分析 (対応あり)の実行
仮説
- 帰無仮説 H_0
- 3科目の好感度の母平均は等しい
- 対立仮説 H_1
- 3科目の好感度の母平均は等しくない
検定統計量 F
\[ F = \frac { \mbox{条件平方和} / \mbox{条件の自由度} } { \mbox{残差平方和} / \mbox{残差の自由度} } \]
\( F \) は,全ての群の母平均が等しいときに,* F分布 * に従う
- 残差平方和
- 全体平均値と群間平均値の差の2乗和
- 条件平方和
- 群間平方和と同じ
検定統計量の実現値
人 <- factor(rep(c("田中","岸", "大引", "吉川", "萩野"),3)) aov(好意度 ~ 科目 + 人) summary(aov(好意度 ~ 科目 + 人))
Call:
aov(formula = 好意度 ~ 科目 + 人)
Terms:
科目 人 Residuals
Sum of Squares 22.53333 45.06667 6.13333
Deg. of Freedom 2 4 8
Residual standard error: 0.875595
Estimated effects may be unbalanced
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 14.7 0.002095 **
人 4 45.07 11.267 14.7 0.000931 ***
Residuals 8 6.13 0.767
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
結果
科目の違いによる平均値差の検定をおこないたかったので, 科目の行を見る:
- F-値が14.7,
- p-値が\( 0.002 < 0.05 \)
で,帰無仮説は棄却されます。
人の行では,
- 人による好感度の差が有意であると示されています。
Fは,分子の自由度が2, 分母の自由度が8のF-分布に従います。
Error 項を指定した分散分析
- formula, error model などに関する説明
aov() 関数にあたえる formula (公式) :
- 人/科目 = 人 + 人:科目
- 人*科目 = 人 + 科目 + 人:科目
- 人:科目 は,人と科目の交互作用
Error 項を指定して分散分析を実行しても同じ結果になります:
summary(aov(好意度 ~ 科目 + Error(人/科目)))
Error: 人
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 4 45.07 11.27
Error: 人:科目
p Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.533 11.267 14.7 0.0021 **
Residuals 8 6.133 0.767
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(aov(好意度 ~ 科目 + 人 + Error(人:科目)))
Error: 人:科目
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 14.7 0.002095 **
人 4 45.07 11.267 14.7 0.000931 ***
Residuals 8 6.13 0.767
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
警告メッセージ:
aov(好意度 ~ 科目 + 人 + Error(人:科目)) で: Error() model is singular
7.2.3 対応の有無による違い
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 2.641 0.112
Residuals 12 51.20 4.267
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 14.7 0.002095 **
人 4 45.07 11.267 14.7 0.000931 ***
Residuals 8 6.13 0.767
参考: 3群以上を比較するとき、2群間の検定(T検定)を使ってはいけない理由
いま、A,B, Cという3つの群があったとします。そこで、2群間の検定を A-B間、 B-C間、C-AC間で有意水準5%で行ったとします。
ここで、「この組み合わせの少なくとも1つは有意差がある」 となる確率を 計算すると(実際にその間に有意差があるなしに拘らず)、 1-(1-0.05)*(1-0.05)*(1-0.05) = 0.14 となります。つまり、 有意水準 5% (=0.05)で検定したつもりが、 この方法では実質的に 14 %で検定している、 つまり 検定力が低下してしまう、というのが理由です。
Tukey の多重比較
TukeyHSD(aov(好意度 ~ 科目 + 人))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = 好意度 ~ 科目 + 人)
$科目
diff lwr upr p adj
線形代数-確率統計 1.4 -0.182381 2.982381 0.0811694
微分積分-確率統計 -1.6 -3.182381 -0.017619 0.0477167
微分積分-線形代数 -3.0 -4.582381 -1.417619 0.0016141
$人
diff lwr upr p adj
岸-荻野 1.3333333 -1.1365377 3.8032044 0.4036928
吉川-荻野 -2.0000000 -4.4698711 0.4698711 0.1226987
大引-荻野 3.0000000 0.5301289 5.4698711 0.0186089
田中-荻野 2.0000000 -0.4698711 4.4698711 0.1226987
吉川-岸 -3.3333333 -5.8032044 -0.8634623 0.0102769
大引-岸 1.6666667 -0.8032044 4.1365377 0.2282769
田中-岸 0.6666667 -1.8032044 3.1365377 0.8766404
大引-吉川 5.0000000 2.5301289 7.4698711 0.0007714
田中-吉川 4.0000000 1.5301289 6.4698711 0.0033834
田中-大引 -1.0000000 -3.4698711 1.4698711 0.6448878
個人の比較には興味がないので,科目についてのみ多重比較
TukeyHSD(aov(好意度 ~ 科目 + 人), "科目")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = 好意度 ~ 科目 + 人)
$科目
diff lwr upr p adj
線形代数-確率統計 1.4 -0.182381 2.982381 0.0811694
微分積分-確率統計 -1.6 -3.182381 -0.017619 0.0477167
微分積分-線形代数 -3.0 -4.582381 -1.417619 0.0016141
7.2.4 平方和の分解と自由度の計算
対応あり/なしでのモデルの違い
- 一元配置 (対応なし)
全体平方和 = 群間平方和 + 郡内平方和
一元配置 (対応あり)
全体平方和 = 条件平方和 + 個人差平方和 + 残差平方和
条件平方和は, 対応なしの群間平方和と同じ
郡内平方和 = 個人差平方和 + 残差平方和 と考える
(全データ <- matrix(c(7,8,9,5,6,
5,4,7,1,3,
8,6, 7,2,5),nrow=5,ncol=3))
[,1] [,2] [,3]
[1,] 7 5 8
[2,] 8 4 6
[3,] 9 7 7
[4,] 5 1 2
[5,] 6 3 5
(科目平均 <- colMeans(全データ))
[1] 7.0 4.0 5.6
(人平均 <- rowMeans(全データ))
[1] 6.666667 6.000000 7.666667 2.666667 4.666667
(全平均 <- mean(全データ))
[1] 5.533333
(全平均行列 <- matrix(rep(全平均,15),nrow=5,ncol=3))
[,1] [,2] [,3]
[1,] 5.533333 5.533333 5.533333
[2,] 5.533333 5.533333 5.533333
[3,] 5.533333 5.533333 5.533333
[4,] 5.533333 5.533333 5.533333
[5,] 5.533333 5.533333 5.533333
(科目平均行列 <- matrix(rep(科目平均,5),nrow=5,ncol=3, byrow=T))
[,1] [,2] [,3]
[1,] 7 4 5.6
[2,] 7 4 5.6
[3,] 7 4 5.6
[4,] 7 4 5.6
[5,] 7 4 5.6
(人平均行列 <- matrix(rep(人平均,3),nrow=5,ncol=3))
[,1] [,2] [,3]
[1,] 6.666667 6.666667 6.666667
[2,] 6.000000 6.000000 6.000000
[3,] 7.666667 7.666667 7.666667
[4,] 2.666667 2.666667 2.666667
[5,] 4.666667 4.666667 4.666667
(全体 <- 全データ - 全平均行列)
[,1] [,2] [,3]
[1,] 1.4666667 -0.5333333 2.4666667
[2,] 2.4666667 -1.5333333 0.4666667
[3,] 3.4666667 1.4666667 1.4666667
[4,] -0.5333333 -4.5333333 -3.5333333
[5,] 0.4666667 -2.5333333 -0.5333333
(条件 <- 科目平均行列 - 全平均行列)
[,1] [,2] [,3]
[1,] 1.466667 -1.533333 0.06666667
[2,] 1.466667 -1.533333 0.06666667
[3,] 1.466667 -1.533333 0.06666667
[4,] 1.466667 -1.533333 0.06666667
[5,] 1.466667 -1.533333 0.06666667
(個人差 <- 人平均行列 - 全平均行列)
[,1] [,2] [,3]
[1,] 1.1333333 1.1333333 1.1333333
[2,] 0.4666667 0.4666667 0.4666667
[3,] 2.1333333 2.1333333 2.1333333
[4,] -2.8666667 -2.8666667 -2.8666667
[5,] -0.8666667 -0.8666667 -0.8666667
(残差 <- 全データ - 全平均行列 - 条件 - 個人差)
[,1] [,2] [,3]
[1,] -1.1333333 -0.1333333 1.26666667
[2,] 0.5333333 -0.4666667 -0.06666667
[3,] -0.1333333 0.8666667 -0.73333333
[4,] 0.8666667 -0.1333333 -0.73333333
[5,] -0.1333333 -0.1333333 0.26666667
(全体平方和 <- sum(全体^2))
[1] 73.73333
(条件平方和 <- sum(条件^2))
[1] 22.53333
(個人差平方和 <- sum(個人差^2))
[1] 45.06667
(残差平方和 <- sum(残差^2))
[1] 6.133333
全体平方和 - (条件平方和 + 個人差平方和 +残差平方和)
[1] -1.421085e-14
結果
全体平方和 = 条件平方和 + 個人差平方和 + 残差平方和 となること確か めた
自由度
- 条件の自由度 = 条件の数 - 1 = 2
- 個人差の自由度 = 人数 - 1 = 4
- 残差の自由度 = 条件の自由度 * 個人差の自由度 = 2 * 4 = 8
- 全体の自由度 = 全データ数 - 1 = 14
全体の自由度 = 条件の自由度 + 個人差の自由度 + 残差の自由度 がなり たつ
7.3 二元配置分散分析 (対応なし)
- 対応のない二元配置分散分析
- 2要因とも対応のある二元配置分散分析
- 1要因のみ対応のある二元配置分散分析
例題
ミネラルウォーターの美味しさの評定に関する実験データ:
- 3銘柄のミネラルウォーターについて,
- 2種類の温度条件のもとで,
- 6通りの条件があり,
- 各条件について5人の評定者,合計30人の評定者による評点
| 冷蔵庫 | 常温 | ||||
| イカアン | ボスビック | ビビッテル | イカアン | ボスビック | ビビッテル |
| 6 | 10 | 11 | 5 | 7 | 12 |
| 4 | 8 | 12 | 4 | 6 | 8 |
| 5 | 10 | 12 | 2 | 5 | 5 |
| 3 | 8 | 10 | 2 | 4 | 6 |
| 2 | 9 | 10 | 2 | 3 | 4 |
検定内容
銘柄の違いや温度の違いにより,おいしさの評点の母平均は異なるか?
データの準備
味 <- c(6,4,5,3,2,10,8,10,8,9,11,12,12,10,10,5,4,2,2,2,7,6,5,4,3,12,8,5,6,4) 温度 <- factor(c(rep("冷蔵庫",15),rep("常温",15))) 銘柄 <- factor(rep(c(rep("イカアン",5),rep("ボスビック",5),rep("ビビッテル",5)),2)) 温度 <- factor(c(rep("冷蔵庫",15),rep("常温",15)))
7.3.1 主効果と交互作用効果
ミネラルウォーターの美味しさに関する実験では,母平均に違いがあると考え られている (対立仮説)
違いの:
- 要因
- 母平均に違いをもたらす原因
- 水準
- ある要因の中に含まれる個々の条件
例題では;
| 要因 | 水準 |
|---|---|
| 温度の違い | 冷蔵、 常温 |
| 銘柄の違い | イカアン、ボスビック、ビビッテル |
二元配置分散分析では、主効果と交互作用効果という2種類の効果を考える
- 主効果
それぞれの要因ごとの効果
一元配置分散分析のときに考えた効果と同じ
- 交互作用効果
2つ以上の要因が組み合わされたときに生じる効果
2つの要因の効果の単純な足し算では説明できない効果
7.3.2 対応のない二元配置分散分析
手順の確認:
- 帰無仮説と対立仮説の設定
- 検定統計量の選択: 分散分析では、検定統計値としてFを利用
- 有意水準 \(\alpha\) の決定: 有意水準は5%、つまりα=0.05とする。この検定は片側検定
検定統計量の実現値を求める
aov関数を用いて実現値を求める
- 帰無仮説の棄却or採択の決定
二元配置分散分析
- 帰無仮説と対立仮説の設定
- 要因A (温度の違い)の主効果
- 帰無仮説 \(H_0\)
- 温度が違ってもおいしさ得点の母平均は等しい(要因Aの主効果はない)
- 対立仮説 \(H_1\)
- 温度の違いによっておいしさ得点の母平均は異なる(要因Aの主効果がある)
- 要因B (銘柄の違い) の主効果
- 帰無仮説 \(H_0\)
- 銘柄が違ってもおいしさ得点の母平均は等しい(要因Bの主効果はない)
- 対立仮説 \(H_1\)
- 銘柄の違いによっておいしさ得点の母平均は異なる(要因Bの主効果がある)
- 要因Aと要因Bの交互作用効果
- 帰無仮説 \(H_0\)
- 温度と銘柄の組み合わせによるおいしさ 得点の影響はない(要因Aと要因Bの交互作用効果はない)
- 対立仮説 \(H_1\)
- 温度と銘柄の組み合わせによるおいしさ 得点の影響がある(要因Aと要因Bの交互作用効果がある)
- 要因A (温度の違い)の主効果
- Fを検定統計量とする
- ここでは有意水準は5%、つまり \(\alpha=0.05\)とする。片側検定である
- 検定統計量の実現値を求める: ここでは、最も一般的なaov関数を用いる
味 <- c(6,4,5,3,2,10,8,10,8,9,11,12,12,10,10,5,4,2,2,2,7,6,5,4,3,12,8,5,6,4) 温度 <- factor(c(rep("冷蔵庫",15),rep("常温",15))) 銘柄 <- factor(rep(c(rep("イカアン",5),rep("ボスビック",5),rep("ビビッテル",5)),2)) summary(aov(味~温度*銘柄))
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.50 21.316 0.00011 ***
銘柄 2 155.0 77.50 24.474 1.61e-06 ***
温度:銘柄 2 15.0 7.50 2.368 0.11515
Residuals 24 76.0 3.17
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
統計検定のための、Rの出力結果からわかること(分散分析編) - Qiita 統計検定のための、Rの出力結果からわかること(回帰分析編) - Qiita
- 帰無仮説の棄却or採択の決定:
- 温度の主効果:5%水準で有意な効果がある (p=0.0011 = 1.1×10-4)
- 銘柄の主効果:5%水準で有意な効果がある (p=1.6×10-6)
- 温度と銘柄の交互作用効果:5%水準で有意な効果はない(p=0.115)
- 関数による交互作用効果の図:
interaction.plot(温度,銘柄,味)
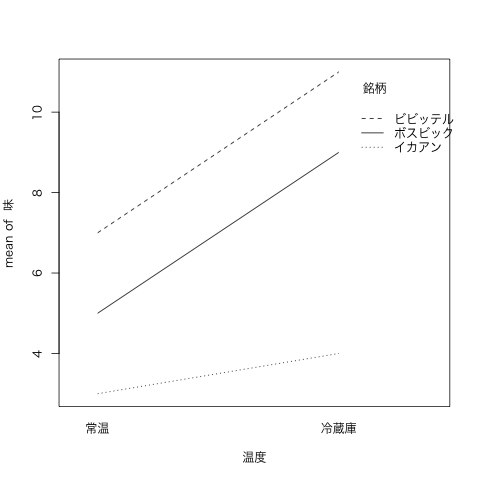
[温度ごとの銘柄と味との関係の図]
interaction.plot(銘柄,温度,味)
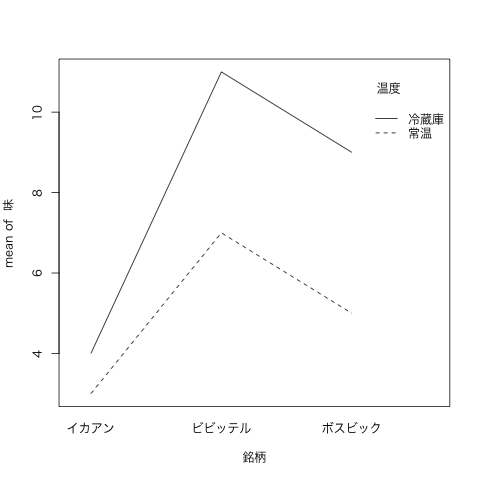
7.3.3 一元配置分散分析との比較
一元配置分散分析をしてみる:
summary(aov(味~温度))
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.50 7.683 0.0098 **
Residuals 28 246.0 8.79
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(aov(味~銘柄))
Df Sum Sq Mean Sq F value Pr(>F)
銘柄 2 155.0 77.50 13.2 1e-04 ***
Residuals 27 158.5 5.87
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
結果
- いずれも有意な差がある,ことは得られているが,
p値に違いがあり,
一元配置の方が大きい
二元配置分散分析の利点
- 二つの要因について同時に検討するだけでなく,
残渣のばらつき(平方和) を減らせるので,
要因毎に有意な結果を得られやすくする
7.4 二要因とも対応のある二元配置分散分析
例題:
ミネラルウォーターの美味しさの5人の評定者による評定データ(前の例題の表に評定者データを加えたもの):
| 冷蔵庫 | 常温 | |||||
| 評定者 | イカアン | ボスビック | ビビッテル | イカアン | ボスビック | ビビッテル |
| 村松 | 6 | 10 | 11 | 5 | 7 | 12 |
| 川崎 | 4 | 8 | 12 | 4 | 6 | 8 |
| 井口 | 5 | 10 | 12 | 2 | 5 | 5 |
| 松中 | 3 | 8 | 10 | 2 | 4 | 6 |
| 城島 | 2 | 9 | 10 | 2 | 3 | 4 |
同じ評定者が、温度と銘柄のそれぞれの要因の組合わせに対して評定を下す
# 変数「味」, 「温度」, 「銘柄」 は前の例題のものを使う 人1 <- factor(rep(c("村松","川崎","井口","松中","城島"),6)) # 評定車の情報 数字1D1 <- factor(rep(1:5,6)) # 評定者名の代わりに数字を使う場合 summary(aov(味~温度*銘柄 # 対応のない場合と同じ +Error(人1+人1:温度+人1:銘柄+人1:温度:銘柄))) # 個人差によるデータの分析 aov(味~温度*銘柄 # 対応のない場合と同じ +Error(人1+人1:温度+人1:銘柄+人1:温度:銘柄)) # 個人差によるデータの分析
Error: 人1
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 4 45 11.25
Error: 人1:温度
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.50 18 0.0132 *
Residuals 4 15.0 3.75
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人1:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
銘柄 2 155 77.5 155 4.01e-07 ***
Residuals 8 4 0.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人1:温度:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
温度:銘柄 2 15 7.5 5 0.039 *
Residuals 8 12 1.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
この例題の場合、「対応がある」ということは『個人差』によるデータのばら つきを分析することができる、ということ。
したがって(個人差のばらつきを除くことにより)、
- 温度の主効果、
- 銘柄の主効果、
温度と銘柄の交互作用の効果の分析が得られる。
上の結果は、いずれも有意であることが示されている
対応なしの場合の分析結果と比較してみましょう。
- 帰無仮説の棄却or採択の決定:
- 温度の主効果:5%水準で有意な効果がある (p=0.0132)(P=0.00011)
- 銘柄の主効果:5%水準で有意な効果がある (p=4.01e-7) (p=1.6×10-6)
- 温度と銘柄の交互作用効果:5%水準で有意な効果がある(p=0.039) 対応なしでは,(p=0.11515) で有意な効果はなかった
7.5 一要因のみ対応のある二元配置分散分析
例題:ミネラルウォーターの美味しさについての評定データ(一つ前の例題の表に評定者データを加えたもの):
| 冷蔵庫 | 常温 | ||||||
| 評定者 | イカアン | ボスビック | ビビッテル | 評定者 | イカアン | ボスビック | ビビッテル |
| 村松 | 6 | 10 | 11 | 斉藤 | 5 | 7 | 12 |
| 川崎 | 4 | 8 | 12 | 和田 | 4 | 6 | 8 |
| 井口 | 5 | 10 | 12 | 寺原 | 2 | 5 | 5 |
| 松中 | 3 | 8 | 10 | 杉内 | 2 | 4 | 6 |
| 城島 | 2 | 9 | 10 | 新垣 | 2 | 3 | 4 |
評定
- 冷蔵庫と常温では異なる評定者が評定する
- 同じ温度に対しては同じ評定者が銘柄のそれぞれの要因の組合わせに対して評 定を下す
# 変数「味」, 「温度」, 「銘柄」 は前の例題のものを使う A1条件 <- rep(c("村松","川崎","井口","松中","城島"),3) A2条件 <- rep(c("斉藤","和田","寺原","杉内","新垣"),3) 人2 <- factor(c(A1条件, A2条件)) 数字ID2 <- factor(c(rep(1:5,3),rep(6:10,3))) # 評定者名の代わりに数字を使う場合 summary(aov(味~温度*銘柄 # 対応のない場合と同じ +Error(人2:温度+人2:温度:銘柄))) # 追加されたオプション
Error: 人2:温度
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.5 9 0.0171 *
Residuals 8 60.0 7.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人2:温度:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
銘柄 2 155 77.5 77.5 5.87e-09 ***
温度:銘柄 2 15 7.5 7.5 0.00504 **
Residuals 16 16 1.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
警告メッセージ:
aov(味 ~ 温度 * 銘柄 + Error(人2:温度 + 人2:温度:銘柄)) で:
Error() model is singular
対応のない分散分析で「残差」としてまとめられていたものを次の要因に分解
- 人2:温度
- 人2と温度の交互効果
- 人2:温度:銘柄
- 人2と温度と銘柄の交互効果
各評定者は同じ温度の条件で3種類の銘柄を飲んでいるため, 個人差の要因となる。
だから、個人差の要因である「人2」と温度の違いの要因をあらわす「温度」 が関係する組み合わせだけを指定する
この分析の結果、「温度」の主効果と「銘柄」の主効果、「温度」と「銘柄」 の交互作用効果に有意差が認められている
拡張
- 同様に、三元配置、四元配置、…要因を増やして分析することが可能
- ただし、要因の数が多いと、分析が複雑になり、結果の解釈が困難になることがあるので注意
分散分析は、基本的に平均値の比較の検定
主効果や交互作用効果の観点からデータにおける値のばらつきの分析が可能